Because of refractive index variations in the air layers just above the ground, atmospheric lensing may significantly deform our view of distant Earth-objects. Similarly, gravitational lensing perturbs our view of the distant Universe and affects our physical understanding of various classes of extragalactic objects. After recalling the basic principles underlying the formation of atmospheric and gravitationally lensed mirages, we describe a simple optical lens experiment which accounts for all types of image configurations observed among presently known gravitational lens systems. Direct images of most of these systems as well as further information on gravitational lensing (bibliography, the present didactical experiments, etc.) may be found on the Gravitational Lensing World Wide Web page at the URL address:

https://vela.astro.uliege.be/grav_lens/grav_lens.html

The didactical experiments proposed in this contribution and most of the figures are adapted from Surdej (1990), Refsdal and Surdej (1992, 1994) and Surdej, Refsdal and Pospieszalska-Surdej (1993, 1995).

1. Atmospheric Lensing

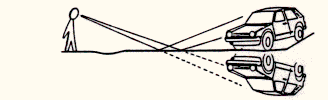
Figure 1 (left), gives a schematic representation of the light ray paths from a distant car (the air close to the ground is hotter than at upper levels). Because air refraction always leads to a bending of light rays towards regions of colder (i.e. more dense) air, several lower and somewhat deformed images of a distant source may result (cf. the car lights in this first example). Figure 1 (right) represents the multiple images of the lights from a distant car, as photographed with a 200 mm focal length camera, along the US 60 road between the towns of Magdalena and Datil near the Very Large Array (New Mexico, USA) on the night of 11 January 1989. The distance between the car and the observers is estimated to be about 10 miles.

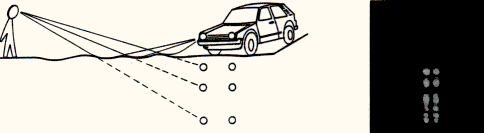
Figure 1: Propagation of light rays above a heated ground between a distant car and an observer (left) and formation of multiple images due to atmospheric lensing (right)

Such terrestrial mirages, usually made of two single images (cf. Figure 2), can actually be seen almost everyday. In addition to significantly affect our view (image deformation, multiplication, etc.) of distant resolved Earth-sources (cf. the resolved images in Figures 1 (right) and 2 (right)), atmospheric lensing is also often responsible for the light amplification of distant unresolved objects located along straight and long roads or across flat countrysides. This was the case, for instance, when looking directly with our naked eyes at the atmospheric mirage illustrated in Figure 1. The car lights then just appeared to consist of a very bright spot ... abnormally bright for a car located at a distance of approximately 10 miles from the observers. Figure 2 (right) illustrates the formation of one lower, inverted and somewhat deformed image of a distant car photographed along the North Panamericana highway between the towns of Pichidangui and La Serena in Chile (2 December 1987).

Figures 3 and 4 illustrate two other examples of atmospheric lensing. They correspond to two different views of the north-south arm of the Very Large Array (VLA) at the National Radio Astronomical Observatory (Socorro, New Mexico, USA). On that early morning of 17 January 1989, the air warmed up by the rising sun was hotter than the ground, leading to the formation of upper-type mirages (cf. the very distinct upper image for the antenna at right in Figure 4).

Given a distribution n(z) for the air refractive index as a function of the vertical height z, it is easy to construct numerically the resulting mirage of a distant source as seen by an observer. This exercise could be the subject of a laboratory in physics for high school students having some basic knowledge in programming (cf. BASIC or FORTRAN). For those students interested in the numerical simulation of such atmospheric mirages, we give hereafter a more thorough physical description of the bending of light rays due to atmospheric lensing (Exercise 1).

1.1 Exercise 1: Physical description of atmospheric lensing

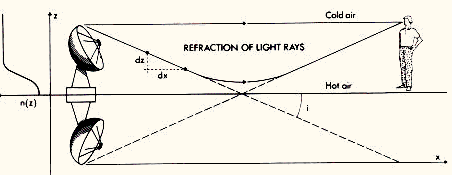
In order to understand in more details the light propagation across a plane parallel atmosphere whose refractive index is affected by a vertical gradient dn/dz, we may apply Fermat's principle according to which the path(s) followed by light between two given points is that (or those) which correspond(s) to an extremum in the propagation time, i.e.

where ds= represents an infinitesimal element along the light trajectory and v=c / n, the velocity of light in the medium with a refractive index n(z) (see Fig. 5). It is easy to show, by means of the Euler-Lagrange equation, that the variational equation (1.1) simply reduces to Descartes's law

where K is a constant and i(z) represents the angle between the tangent to the light ray and the horizontal direction. It is then straightforward to derive the expression for the small angle increment of the ray between two neighbouring points whose abscissae are x and x+dx. For a small but finite value of dx and small inclination angle i, we find with a good approximation that

This relation is very useful in order to construct numerically the trajectory of light rays across an atmosphere characterized by a refractive index distribution n(z). In doing so, one finds that under special circumstances (cf. specific refractive index distributions n(z), source distance, etc.) there may exist several geodesics between the source and the observer, resulting in the possible formation of multiple images. It is also interesting to note that because of the difference in the geometric lengths and light velocities (c / n(z)) along two geodesics, there will generally be a delay between the arrival times of a signal from the source (cf. a hypothetical light flash) as seen by a distant observer. This time delay depends of course on the refractive index distribution n(z) and also on the absolute distance between the source and the observer.

Finally, let us remark that because atmospheric lensing preserves surface brightness, just as in the case of gravitational lensing, the amplification of a mirage luminosity is simply given by the ratio of the solid angle of the observed (lensed) image to that of the (unlensed) source. Therefore, in addition to affecting significantly our view (image deformation, multiplication, etc.) of distant resolved Earth-sources, atmospheric lensing is also often responsible for the light amplification of distant unresolved objects located along straight and long roads or across flat countrysides.

As we shall see in the remainder, there exist quite a few other similarities between atmospheric and gravitational lensing.