1. Introduction
|
| The Old Halo metallicity gradient: the trace of a self-enrichment process |
Institut d'Astrophysique et de Géophysique, Université de
Liège, 5, Avenue de Cointe, B-4000 Liège, Belgium
* Chercheur qualifié au Fonds National de la Recherche
Scientifique (Belgium)
| Abstract |
Based on a model of globular cluster self-enrichment published in a previous paper, we present an explanation for the metallicity gradient observed throughout the galactic Old Halo. Our self-enrichment model is based on the ability of globular cluster progenitor clouds to retain the ejecta of a first generation of Type II Supernovae. The key point is that this ability depends on the pressure exerted on the progenitor cloud by the surrounding protogalactic medium and therefore on the location of the cloud in the protoGalaxy. Since there is no significant (if any) metallicity gradient in the whole halo, we also present a review in favour of a galactic halo partly build via accretions and mergers of satellite systems. Some of them bear their own globular clusters and therefore "contaminate" the system of globular clusters formed "in situ", namely within the original potential well of the Galaxy. Therefore, the comparison between our self-enrichment model and the observational data should be limited to the genuine galactic globular clusters, the so-called Old Halo group.
| Table of contents |
1. Introduction
|
Galactic globular clusters (hereafter GCs)
are fossil records of the formation of the Galaxy.
The understanding of their formation process would certainly shed light
on the early galactic evolution. However,
at the present time, there is no widely accepted theory of GC formation.
In Parmentier et al. (1999) (hereafter Paper I), we suggest a
formation scenario based on a self-enrichment process
such as proposed by Cayrel (1986)
and further developed by Brown et al. (1991, 1995).
Our self-enrichment scenario takes place within the Fall & Rees (1985)
description of the protoGalaxy, namely cold clouds embedded in a
hot protogalactic background. These cold clouds are assumed
to be the progenitors of galactic halo GCs.
Since they are made up of primordial gas,
the main advantage of a self-enrichment scenario is that
it explains in parallel the formation of the clusters and the origin
of their metal contents.
The main target of Paper I was to
demonstrate conclusively that the gaseous
progenitors of galactic halo GCs are able
to sustain a few hundreds of Type II Supernovae (hereafter SNII)
without being disrupted.
This result is in contrast with the widespread idea according to which
a few supernovae are able to disrupt a Proto-Globular Cluster Cloud
(hereafter PGCC).
Furthermore, the large number of SNeII allowed by our model
can explain the amount
of metals currently observed in galactic halo globular clusters,
and this without any requirement of pre-enrichment of the gas.
The aim of the present paper is to explore further an
interesting consequence of Paper I, which is also the main
difference existing between our self-enrichment model and the one
developed by Brown et al. (1995).
The metallicity that a PGCC can reach through self-enrichment depends on
the pressure exerted by the medium surrounding the progenitor cloud
and, therefore, on the cloud location in the protoGalaxy.
The deepest in the protoGalaxy the PGCC is located, the highest
the final metallicity induced by self-enrichment will be.
Therefore, we expect to find a metallicity gradient throughout
the galactic halo.
The paper is organised as follows.
In Sect. 2,
we briefly review the self-enrichment model
presented in Paper I, focusing on the link
between the final metallicity of the PGCC and the pressure exerted
on it by the surrounding hot protogalactic background.
In Sect. 3, we examine the
different arguments suggesting the existence of
halo substructures, in order to isolate
to which one the self-enrichment model can be safely compared.
In Sect. 4, we compare the model with
the observations.
Sect. 5 explores the putative link between GC
metallicities and their perigalactic distances.
Finally, we present our conclusions in Sect. 6.
2. Self-enrichment model
|
According to Fall & Rees (1985), galactic halo GCs were formed
during the collapse of the protoGalaxy.
During this collapse, a thermal instability triggers the development of
a two-phase structure, namely
cold and dense clouds in pressure equilibrium with a hot and diffuse
protogalactic background.
The temperature of the clouds is assumed to remain at a value of
104 K,
where the cooling rate drops sharply in a metal-free medium.
Their masses scale as the Jeans mass of a pressure-truncated
spherical cloud with a temperature
 104 K.
Since this is of the same order of magnitude
(
104 K.
Since this is of the same order of magnitude
(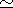 106,M
106,M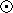 ) as the GC masses,
Fall & Rees (1985) identify these cold clouds
with the progenitor clouds of GCs (however, this temperature,
and therefore, the characteristic mass, is preserved only if there
is a UV flux able to prevent any H2 formation, the
main coolant in a metal-free gas below 104 K).
As already mentioned, the PGCCs are assumed to be metal-free and the
formation process must therefore explain how the metals are provided within
each cloud. Within this context, the self-enrichment hypothesis was
proposed by Cayrel (1986) and further developed by Brown et al. (1991,
1995). A first generation of stars is assumed to form in the central
regions of the progenitor cloud. When the massive stars of this first
generation explode as SNeII,
all the cloud material is progressively swept in an expanding supershell.
This supershell gets chemically enriched with the metals released
by the exploding massive stars. Since it is a
compressed layer of gas, it constitutes a dense medium where
the formation of a second generation of stars is triggered.
Under favourable conditions (see Brown et al., 1995)
these second generation stars, formed in the chemically
enriched supershell, can recollapse and form a GC.
Therefore, the first generation SNeII provide the GC metals and
trigger the formation of the GC stars.
) as the GC masses,
Fall & Rees (1985) identify these cold clouds
with the progenitor clouds of GCs (however, this temperature,
and therefore, the characteristic mass, is preserved only if there
is a UV flux able to prevent any H2 formation, the
main coolant in a metal-free gas below 104 K).
As already mentioned, the PGCCs are assumed to be metal-free and the
formation process must therefore explain how the metals are provided within
each cloud. Within this context, the self-enrichment hypothesis was
proposed by Cayrel (1986) and further developed by Brown et al. (1991,
1995). A first generation of stars is assumed to form in the central
regions of the progenitor cloud. When the massive stars of this first
generation explode as SNeII,
all the cloud material is progressively swept in an expanding supershell.
This supershell gets chemically enriched with the metals released
by the exploding massive stars. Since it is a
compressed layer of gas, it constitutes a dense medium where
the formation of a second generation of stars is triggered.
Under favourable conditions (see Brown et al., 1995)
these second generation stars, formed in the chemically
enriched supershell, can recollapse and form a GC.
Therefore, the first generation SNeII provide the GC metals and
trigger the formation of the GC stars.
Supernova energetics has been a major criticism of
the GC self-enrichment hypothesis. However, the main target of Paper I was
to conclusively demonstrate that a PGCC is not
necessarily disrupted by SNII explosions.
Our self-enrichment model is detailed in Paper I.
Suffice it to say that we compute, for a given hot protogalactic
background pressure, the supershell
velocity during the sweeping of the PGCC as a function of the explosion
rate. Based on this
result, we compare the kinetic energy of the supershell with
the binding energy of the PGCC in order to get the maximum number of SNeII
the cloud is able to sustain.
Whatever the value of Ph,
the pressure exerted by the hot protogalactic background
on the cloud, we find that a PGCC can sustain about 200 SNeII.
Such a large number of SNeII
can provide the amount of metals observed in galactic halo GCs.
The results of Paper I are summarized in
Table 1 (see
Sect. 4.2
for a justification of the Ph values).
Clearly, GC halo metallicities can be reached through self-enrichment.
We see from Table 1 that
the higher the external pressure is, the higher the metallicity will be.
Indeed, since the dynamical constraint leads to
a constant SNII number, assuming a given Initial Mass Function
(namely a Salpeter
one) and a given stellar mass range, a constant amount of metals
(independent of Ph) is
released by the first generation massive stars.
Since the PGCC mass decreases with increasing external pressure
(the Jeans mass scales as Ph-1/2,
Eq. (5) in Paper I),
the PGCCs embedded in a higher pressure medium, namely
located deeper in the protoGalaxy, reach higher final metallicities.
This self-enrichment model, contrary to the one developed by
Brown et al. (1995),
implies a metallicity gradient throughout the galactic halo.
At first sight, there is no confirmation of this self-enrichment model by
the observational data. The galactic halo exhibits no significant
metallicity gradient
(see Fig. 1; data are based on Harris
19961)
However, according to Zinn (1993), the galactic halo is
composed of two distinct subpopulations of GCs, what he calls
an Old Halo and a Younger Halo.
The next section presents a review of the evidence supporting Zinn's idea.
1 Data updated 1999 June 22 at
http://physun.physics. mcmaster.ca/Globular.html.
3. Two populations of galactic halo GCs
|
According to Zinn (1985), the galactic Globular Cluster System
(hereafter GCS) includes two subsystems: the
disk GCs 2 ([Fe/H] > - 0.8) and the halo GCs
([Fe/H] < - 0.8).
Both groups also differ in their mean rotational velocity and
spatial distribution about the galactic center.
Globular cluster classification has now gone a step further, and
the halo subsystem could be itself divided into two groups.
2 Due to their high concentration near the
galactic center, these metal-rich clusters, at least those located
within the inner ~4 kpc of the Galaxy, are now thought to
be associated with the galactic bulge
rather than with the disk (Minnitt 1995, Côté 1999).
3.1. Horizontal Branch morphology
|
Zinn (1993) sorts the galactic halo GCs
into two groups according to their Horizontal Branch
(hereafter HB) morphology.
The HB morphology, namely the colour distribution of the
stars located along the HB, can be described by the
index C = (B-R)/(B+V+R) where B, V and R are respectively the
numbers of blue, variables and red HB stars. This index therefore ranges
from - 1 for a purely red HB to +1 for a purely blue one.
The morphology of the HB is essentially driven by the metallicity
of the cluster. As such, [Fe/H] is the first parameter
that governs
the HB morphology. However, it has long been known that some clusters
with similar [Fe/H] values present very different HB morphologies
(e.g. M 13 and M 3, NGC 288 and NGC 362).
This is the so-called second parameter effect: a
second parameter (at least), in addition to metal abundance,
is needed to explain the HB morphology.
Zinn (1993) notices that,
while the inner halo GCs (D < 8 kpc, where D
is the galactocentric distance) exhibit a
tight relationship between HB morphology and [Fe/H],
the outer halo GCs (D > 8 kpc) show a large scatter
in the same relation. Hence, the requirement of a
second parameter to explain the HB morphology is
mostly needed for GCs located beyond the solar circle.
Since, at a given metallicity, these clusters have also
redder HBs than the inner halo GCs,
Zinn (1993) divides the galactic halo GCs into two groups:
the inner halo GCs are classified as Blue Horizontal Branch (BHB) clusters,
while the clusters whose HB types are 0.4 redder than
their inner halo counterparts (equal metallicity) are labelled as Red
Horizontal Branch (RHB) clusters. As mentioned above,
these RHB clusters are mostly located outside the solar circle.
This link between the influence of the second parameter and the
galactocentric distance indicates that the second parameter problem must be
related in some way to the formation of the Galaxy (Searle & Zinn 1978).
According to Lee et al. (1993), the most promising candidate for
this second parameter is age. If age is indeed the second
parameter, then, at a given metallicity, a RHB GC
is younger than its BHB counterpart.
Therefore, Zinn (1993) labels the BHB group and
the RHB group respectively "Old" Halo and "Younger" Halo.
To explain these putative age differences,
and since the "Younger" Halo GCs are mostly located in the outer part of
the halo, Zinn (1993) suggests that the two groups were formed in two
different ways.
The "Old" Halo (hereafter OH) GCs would have been formed during
the rapid collapse of the protogalactic cloud, while the "Younger"
Halo (hereafter YH) GCs would have been
formed in satellite systems, such as dwarf galaxies,
which evaded the protogalactic collapse
and which were later accreted by the Galaxy.
3.2. GC Ages
|
The hypothesis that RHB clusters are younger than their BHB counterparts
relies on the implicit assumption that age is the only
second parameter driving the HB morphology, in addition to metallicity.
Therefore, it is interesting to wonder if age determinations based
on the luminosity or the colour of the Main Sequence Turn-Off confirm
such an hypothesis.
The nature of the second parameter remains a much debated question
(for contrasting points of view, see the reviews by Stetson et al. 1996
and Sarajedini et al. 1997). Chaboyer et al. (1996) find that RHB clusters
are on average 2-3 Gyr younger than BHB clusters, which is consistent
with age being the dominant second parameter.
This point of view has been reinforced
by other studies where some clusters have been found
to be significantly younger than the bulk of the other galactic halo GCs.
These are Pal 12 (Stetson et al. 1989),
Rup 106 (Buonanno et al. 1993), Arp 2 (Buonanno et
al. 1995), IC 4499 (Ferraro et al. 1995), Pyxis (Sarajedini
& Geisler 1996), Pal 14 (Sarajedini 1997),
Pal 5 (Buonanno et al. 1998), the outer halo GCs Pal 3,
Pal 4, Eridanus (Stetson et al. 1999), NGC 362, 1261, 1851,
2808 (Rosenberg et al. 1999).
All these younger GCs are RHB clusters and are located
outside the solar circle, where the second parameter effect is dominant.
Zinn's idea is therefore strengthened.
However, according to Rosenberg et al. (1999),
three RHB clusters (NGC 3201, NGC 5272 and possibly
NGC 4590) have not been proven to be younger.
As a result, age appears to be one of the most appealing
second parameter candidates
(Ferarro et al. 1995, Chaboyer et al. 1996, Stetson et
al. 1999), but an additional parameter is probably at work in a
minority of clusters.
3.3. Kinematic Differences
|
Whatever the second parameter is, the concept of two genuinely
distinct halo subsystems gets some support from the presence
of a kinematic difference between the YH and the OH groups.
While the mean galactic rotation of the OH group is clearly prograde,
it is close to zero, perhaps even sligthly retrograde,
for the YH group (Zinn 1993, Da Costa & Armandroff 1995,
Odenkirchen et al. 1997).
This result has been recently confirmed by the work performed
by Dinescu et al. (1999).
Based on the most complete compilation of GC proper motions
existing up to now, they compute the orbits of 38 GCs.
Although a sharp truncation between the
different orbital parameters does not appear,
they show that, on the average, the "Old" Halo and the "Younger" Halo
GCs exhibit some differences in their kinematics and their orbit shapes.
The "Younger" Halo (RHB) group presents, on the average,
a smaller rotational velocity, larger velocity dispersions,
higher orbital energies, higher apogalactic distances
(Da 10 kpc) and higher
excentricities than the "Old" Halo (BHB) group.
If the RHB group represents an accreted component of our Galaxy,
the mean rotational velocity suggests that a significant
fraction of the outer GCs came from one or more
ancestral objects on retrograde orbits.
10 kpc) and higher
excentricities than the "Old" Halo (BHB) group.
If the RHB group represents an accreted component of our Galaxy,
the mean rotational velocity suggests that a significant
fraction of the outer GCs came from one or more
ancestral objects on retrograde orbits.
3.4. Dwarf galaxies accretion
|
Dwarf irregular and dwarf
spheroidal galaxies, at least the most massive ones, also host their own
GCS (e.g. the Magellanic Clouds, Fornax).
Interestingly, in a plot of [Fe/H] vs C,
the HB morphology index, some of the Large Magellanic Cloud (hereafter LMC)
GCs fall among the outer halo GCs (Da Costa 1993).
If age is accepted as the dominant second parameter,
then these clusters are younger than the inner galactic halo GCs.
This is in agreement with the presence in the LMC of young
clusters whose masses are within the galactic GC mass range
(Elson & Fall 1988, Meylan & Heggie 1997).
The hypothesis that the halo was partly built
via accretion was underlined by several authors.
Lin & Richer (1992) suggest that Rup 106 and Pal 12,
two RHB clusters known to be younger than other GCs with
similar metallicity (see Sect. 3.2),
were tidally captured by the Galaxy from the Magellanic Clouds
during their recent perigalacticon passage.
A similar argument holds for Pyxis, another RHB and young cluster
(Irwin et al.1995).
The association between some RHB/younger GCs and streams
(alignments along great circles over the sky
which could arise from the disruption of MW satellites)
is advocated in Majewski (1994) and Fusi Pecci et al. (1995).
All these GCs could therefore have been born well apart from
the original protoGalaxy, joining our Galaxy through later infall events.
As such, they are not indicative of the early formation of the
galactic halo.
Furthermore, Nature currently provides us with an example of
satellite accretion.
The Sagittarius dwarf spheroidal galaxy, the closest satellite of
the Galaxy, is currently undergoing strong tidal distorsions
indicating that it will probably be disrupted
and absorbed by the Milky Way (Ibata et al. 1997, Johnston et al. 1999).
Based on both positional and kinematic data, 4 GCs (M 54, Arp 2,
Ter 8 with halo metallicities and Ter 7 with disk metallicity)
unambigously belong to the Sgr dwarf (Ibata et al. 1997).
These GCs are therefore being incorporated into the galactic halo
and as such constitute a source of "contamination" of the genuine
galactic GCs, the real tracers of the early evolution of the Galaxy.
Ibata et al. (1997) also strongly suspect the presence
of a dark halo around the Sgr dwarf.
Indeed, dwarf spheroidals are among the most dark-matter dominated
systems known (Mateo 1998) and dwarf irregulars are significanly
more dark-matter dominated than are large spirals (Carignan et al. 1990).
The presence of dark
matter halos around the Milky Way satellites, denser than what is found
around large spirals, could induce some differences in the star and GC
formation mechanisms compared to what occurs in the protoGalaxy
(Larson 1993).
3.5. Spatial distribution
|
Finally, considering the GCs with [Fe/H] < - 1 (in order to remove the obvious disk clusters), Hartwick (1987) notes that their spatial distribution can be described in terms of two subsystems: an inner flattened distribution and an outer more spherical distribution.
3.6. What does this all mean ?
|
The convergence of all the differences mentioned above (HB morphologies,
ages, kinematic data, galactocentric distances and
spatial distributions around the galactic center)
between BHB and RHB GCs adds weight to
the claim that they form two genuinely distinct groups.
The existence of two main substructures in the galactic halo implies
that a hybrid picture could conveniently describe its formation
(Stetson et al. 1996, Sarajedini et al. 1997, Rosenberg et al. 1999).
The inner part, populated by BHB GCs, would have been formed
over a relatively short period of time during the collapse of the
protoGalaxy (Eggen, Lynden-Bell & Sandage 1962),
while the outer part, which includes most of the RHB GCs, was mainly
built via accretion and mergers of
satellite systems in a still ongoing process (Searle & Zinn 1978).
In this case, the outer halo objects would actually bear little direct
relevance to the formation history of the main part of the Galaxy.
As such, they should not be considered when comparing our
self-enrichment model to the observational situation
(see Sect. 4.1).
To disentangle the genuine galactic GCs from those formed in
satellite systems and accreted afterwards, Zinn (1993) suggests
to rely on a HB morphology criterion. As illustrated above,
this approach is indeed fruitful since many RHB
clusters exhibit peculiarities, such as lower ages than their
BHB counterparts. However, the GCSs
of dwarf galaxies are not exclusively composed of young GCs
and, consequently, the actual situation is certainly more complicated.
A LMC cluster, Hodge 11, is as old as the inner halo GCs
(Mighell et al ,1996). The Sagittarius cluster system will contribute to
both the YH (Ter 7 and Arp 2) and OH (Ter 8 and M 54)
groups (Da Costa & Armandroff 1995).
Therefore, the OH subsystem may also contain some accreted objects and
is not a pure sample of GCs formed during the collapse
of the protoGalaxy main body.
NGC 2419 and M 5 might be some of these interlopers.
NGC 2419 is the only BHB GC located beyond the Magellanic Clouds.
While it has the same age as M 92, an inner halo GC with
similar metallicity (Harris et al ,1997),
it is quite difficult to imagine that this metal-poor cluster
formed in the inner halo and then migrated into the far outer one.
The same problem stands for NGC 5904 (M 5), an outer halo BHB GC
currently visiting the inner regions of the galactic halo
(Dinescu et al. 1999).
Clearly, Zinn's classification needs refinements but nevertheless
constitutes a first step in understanding the
different processes at work during the whole halo history.
Therefore, in what follows,
we mainly rely on this BHB/RHB division.
To close this section, we note that some of the trends presented by GCs are
also reproduced by field halo stars.
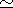 10 kpc form a younger group
with a larger age dispersion than the inner part of the stellar halo.
10 kpc form a younger group
with a larger age dispersion than the inner part of the stellar halo.
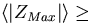 5 kpc,
where ZMax is the maximum height reached by the stars
above the galactic plane) and a "low halo"
(
5 kpc,
where ZMax is the maximum height reached by the stars
above the galactic plane) and a "low halo"
(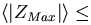 5 kpc).
The "high halo", which
should be dominated by the accreted population, is found
in net retrograde rotation. In contrast, the "low halo" is in
prograde rotation.
5 kpc).
The "high halo", which
should be dominated by the accreted population, is found
in net retrograde rotation. In contrast, the "low halo" is in
prograde rotation.
4. The metallicity gradient
|
4.1. Importance of the OH/YH division
|
The whole galactic GCS exhibits a metallicity gradient interpreted
as a disk-halo dichotomy, namely, the gradient
is mainly driven by the high metallicity clusters (disk component:
[Fe/H] > - 0.8) located within
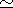 8 kpc from the galactic center
(Djorgovski & Meylan 1994).
The halo group itself ([Fe/H] < - 0.8) presents no clear
metallicity gradient
(see Fig. 1).
However, Sect. 3
provides several arguments supporting a further meaningful division,
mainly based on a BHB/RHB (OH/YH) classification,
of the halo system. As a result, the situation must be reconsidered.
8 kpc from the galactic center
(Djorgovski & Meylan 1994).
The halo group itself ([Fe/H] < - 0.8) presents no clear
metallicity gradient
(see Fig. 1).
However, Sect. 3
provides several arguments supporting a further meaningful division,
mainly based on a BHB/RHB (OH/YH) classification,
of the halo system. As a result, the situation must be reconsidered.
Following Zinn (1993), the OH GCs are formed during the
monolithic collapse of the protogalactic cloud while the
more remote YH GCs are formed in fragments that escape the
protogalactic collapse. Later on, these fragments evolve into satellite
systems, e.g. dwarf galaxies, bearing their own GCs into the
galactic halo once they are accreted by the Milky Way.
These dwarf galaxies GCs are therefore added to the
original galactic GCs.
According to the model exposed in Paper I,
the metallicity [Fe/H], induced by the self-enrichment process, is related
to the hot protogalactic background pressure Ph
by (see Table 1):

| (1) |
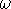 Cen,
the most peculiar galactic GC
(e.g. large mass, iron-peak element inhomogeneities
in sharp contrast with the monometallicity observed in other GCs).
These peculiarities could be the result of the merger of two GCs
(Jurcsik 1998) or of the accretion of a dwarf galaxy
tidally stripped of its stellar envelope (Majewski 2000).
Cen,
the most peculiar galactic GC
(e.g. large mass, iron-peak element inhomogeneities
in sharp contrast with the monometallicity observed in other GCs).
These peculiarities could be the result of the merger of two GCs
(Jurcsik 1998) or of the accretion of a dwarf galaxy
tidally stripped of its stellar envelope (Majewski 2000).  logD
logD with decreasing metallicity over the range
[Fe/H]
with decreasing metallicity over the range
[Fe/H]  -0.8
to [Fe/H]
-0.8
to [Fe/H]  -2.4.
-2.4.
4.2. Pressure profile of the hot
protogalactic background
|
Concerning this point, the situation is rather complex since there
is obviously no agreement about the scaling of the Ph(D)
relation in the literature.
The luminous components of galaxies form through the collapse of gas
in gravitationally dominant halos of dark matter.
The density profile of such a halo
is conveniently described as a singular isothermal sphere
(White & Kauffmann 1994):

| (2) |

| (3) |
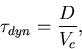
| (4) |

| (5) |
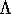 is the cooling function (Sutherland & Dopita 1993).
is the cooling function (Sutherland & Dopita 1993).
 dyn <
dyn <  cool,
the gas undergoes quasi-static contraction, but
once
cool,
the gas undergoes quasi-static contraction, but
once  cool <
cool <  dyn,
the gas cloud can no longer
maintain itself in quasi-static equilibrium and the collapse
proceeds on a free-fall timescale (e.g. Rees & Ostriker 1977).
dyn,
the gas cloud can no longer
maintain itself in quasi-static equilibrium and the collapse
proceeds on a free-fall timescale (e.g. Rees & Ostriker 1977).
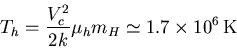
| (6) |
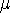 h
is the mean molecular weight (~0.6 for a
primordial ionized plasma, with X
h
is the mean molecular weight (~0.6 for a
primordial ionized plasma, with X 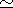 0.76
and Y
0.76
and Y 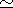 0.24).
At this temperature, the value of the cooling function
0.24).
At this temperature, the value of the cooling function
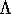 is 4.8 × 10-24 erg cm3 s-1 (Sutherland & Dopita 1993).
Combining Eqs. (4 - 6), we have
is 4.8 × 10-24 erg cm3 s-1 (Sutherland & Dopita 1993).
Combining Eqs. (4 - 6), we have

| (7) |
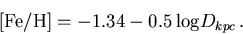
| (8) |
 cool
cool 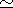
 dyn.
The model proposed by Murray & Lin (1992) is slightly different.
It relies on the
dyn.
The model proposed by Murray & Lin (1992) is slightly different.
It relies on the  cool
cool 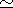
 dyn condition
and also on the hypothesis of hydrostatic equilibrium for the hot gas:
dyn condition
and also on the hypothesis of hydrostatic equilibrium for the hot gas:
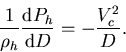
| (9) |
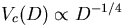 .
It should be noted that the value of the exponent
ensures that the temperature of the hot gas obeys to Eq. (6)
with Vc and Th
depending on D (their Eq. (3.9)).
In contrast with Fall & Rees (1985),
their pressure profile for the hot protogalactic
background scales as D-2:
.
It should be noted that the value of the exponent
ensures that the temperature of the hot gas obeys to Eq. (6)
with Vc and Th
depending on D (their Eq. (3.9)).
In contrast with Fall & Rees (1985),
their pressure profile for the hot protogalactic
background scales as D-2:

| (10) |
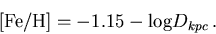
| (11) |
 dyn and
dyn and
 cool
scale respectively as D (Eq. (4)) and as D2
(Eq. (5)). There is thus a "critical" galactocentric
distance Dcrit such that
cool
scale respectively as D (Eq. (4)) and as D2
(Eq. (5)). There is thus a "critical" galactocentric
distance Dcrit such that
 cool <
cool <  dyn when
D < Dcrit:
dyn when
D < Dcrit: cool
cool 
 dyn
when D
dyn
when D  Dcrit:
Dcrit:
 cool and
cool and
 dyn over
the whole galactic halo and, therefore, this property can no longer
be used to determine Ph(D).
However, it is interesting to note that the steady rise of the ratio
dyn over
the whole galactic halo and, therefore, this property can no longer
be used to determine Ph(D).
However, it is interesting to note that the steady rise of the ratio
 cool /
cool /  dyn
with galactocentric distance is a property found in the halos of giant
ellipticals, e.g. M 87 (Fabricant et al. 1980).
dyn
with galactocentric distance is a property found in the halos of giant
ellipticals, e.g. M 87 (Fabricant et al. 1980).  ),
but not from the same hypotheses! This illustrates the difficulty
to derive an expression for the
metallicity gradient from the self-enrichment model.
),
but not from the same hypotheses! This illustrates the difficulty
to derive an expression for the
metallicity gradient from the self-enrichment model.
4.3. Discussion
|
In Fig 2.
we compare the results given by Eq. (8)(dashed line) and Eq. (11)
(plain line) to the observational data.
The region of interest, namely where the bulk of the OH
group is located, is the galactocentric range 1 to 30 kpc.
The metallicity intervals predicted by Eqs. (8) and (11)
for these values of the galactocentric distance are respectively
[-2 dex, -1.35 dex] and
[-2.65 dex, -1.15 dex].
The second model (self-enrichment model
combined with 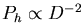 ,
in this case the Murray & Lin (1992)
pressure distribution) is a better description for the
observed metallicity range (see Table 2).
,
in this case the Murray & Lin (1992)
pressure distribution) is a better description for the
observed metallicity range (see Table 2).
The theoretical metallicity gradients corresponding to Eqs. (8)
(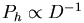 ) and (11)
(
) and (11)
(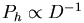 )
are respectively
)
are respectively
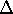 [Fe/H]/
[Fe/H]/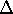 logD = -0.5 dex
and -1 dex.
It is not straightforward to compare these results
with the observational gradient because
of the rather high dispersion in the [Fe/H] vs logD plot,
partly due to measurement errors in [Fe/H] and logD.
The observed dispersion can also be explained by
the GC orbital motions.
Indeed, our model predicts a relation
between the GC metallicities and the galactocentric distances of
their formation site. But the GCs were carried
away from their formation sites through their orbital motions.
The initial radial distribution of globular cluster abundances
has therefore been modified but we can only use the current one.
A least-squares fit to the OH+noHBR groups, which takes into
account the uncertainties in both coordinates (Press et al. 1992),
yields:
logD = -0.5 dex
and -1 dex.
It is not straightforward to compare these results
with the observational gradient because
of the rather high dispersion in the [Fe/H] vs logD plot,
partly due to measurement errors in [Fe/H] and logD.
The observed dispersion can also be explained by
the GC orbital motions.
Indeed, our model predicts a relation
between the GC metallicities and the galactocentric distances of
their formation site. But the GCs were carried
away from their formation sites through their orbital motions.
The initial radial distribution of globular cluster abundances
has therefore been modified but we can only use the current one.
A least-squares fit to the OH+noHBR groups, which takes into
account the uncertainties in both coordinates (Press et al. 1992),
yields:
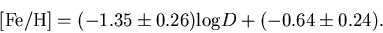
| (12) |
 logD=1.
This leads to an error of ±0.4 in logD.
We caution that, by doing so,
the errors are assumed to be normally distributed. This is
probably not the case for logD,
since the galactocentric distances of the
formation sites are replaced by the current galactocentric distances.
Therefore, the dispersion in logD cannot
be attributed solely to measurement errors. The slope of Eq. (12)
is consistent with the one of Eq. (11) at the 1.3
logD=1.
This leads to an error of ±0.4 in logD.
We caution that, by doing so,
the errors are assumed to be normally distributed. This is
probably not the case for logD,
since the galactocentric distances of the
formation sites are replaced by the current galactocentric distances.
Therefore, the dispersion in logD cannot
be attributed solely to measurement errors. The slope of Eq. (12)
is consistent with the one of Eq. (11) at the 1.3
 level,
while it is different from the slope given by Eq. (8)
at the 3.3
level,
while it is different from the slope given by Eq. (8)
at the 3.3 level. As a conclusion,
Eq. (1) better describes the observed radial
distribution of GC metallicities when it is combined with
a pressure profile scaling as D-2 (Eq. (11)) rather
than D-1 (Eq. (8)).
However, Eq. (11) somewhat underestimates the
mean observed metallicity at a given galactocentric distance.
This can be due to:
level. As a conclusion,
Eq. (1) better describes the observed radial
distribution of GC metallicities when it is combined with
a pressure profile scaling as D-2 (Eq. (11)) rather
than D-1 (Eq. (8)).
However, Eq. (11) somewhat underestimates the
mean observed metallicity at a given galactocentric distance.
This can be due to:
5. Were GCs formed near their
perigalacticon ?
|
The initial halo metallicity gradient
was severely altered by the accretion of GCs formed in dwarf and/or
irregular galaxies. The genuine Milky Way GCs moving away
from their formation sites is another cause of alteration.
It would be very useful to know the galactocentric distances at which the
GCs were formed, in order to better evaluate the validity of
Eqs. (8) and (11).
In Sect. 4.3,
it was suggested that GCs might have formed
deeper in the galactic halo than their current location.
However, we caution that this result relies on the self-enrichment
model and on the assumed pressure distribution.
Therefore, this outcome cumulates uncertainties from both
and it certainly does not stand on a firm support.
Even so, previous papers already suggest that the correlation
between [Fe/H] and logDp, where Dp
is the perigalactocentric distance of the GCs, may be stronger than
between [Fe/H] and logD.
Freeman & Norris (1981) notice "a clear gradient in the
[Fe/H]-Dp plane".
According to them, this may be a hint that the clusters
did form near perigalacticon. Van den Bergh (1995) also notes
that the GC metallicity correlates somewhat more strongly with
Dp
than it does with the present GC galactocentric distances.
Nevertheless, the method used to derive these perigalactic distances
is somewhat problematic. It assumes that the current GC tidal
radius is mostly set by the galactic tidal field at the closest
approach of the cluster to the galactic center, namely the
perigalacticon (King 1962). As a result,
tidal radii of well observed GCs are used to estimate
their perigalactic distances. By so doing, the GC internal processes,
especially the two-body relaxation, are neglected (Meziane & Colin 1996).
These internal processes lead to a replenishment of the outer regions
of the cluster between two perigalactic passages and therefore modify
the outer radius set at the perigalacticon.
Thus, it is dangerous to rely on the current outer radius of GCs to derive
their perigalactocentric distances.
In order to avoid this problem, perigalactic distances
derived from the computation of GC orbits (Dinescu et al. 1999)
are used in Figs. 3 (all GCs with known
perigalactic distances) and 4 (OH GCs).
Another cluster, NGC 6522 (Terndrup et al. 1998),
is added to Dinescu's list.
The sample is by far smaller than in Van den Bergh (1995).
This is due to the necessity to know the proper motions in order
to compute the GC orbits in a given galactic potential.
The (logDp, [Fe/H]) plot
(Fig. 4) does not appear tighter
than the (logD, [Fe/H]) one
(Fig. 2).
The linear Pearson correlation coefficient in
Fig. 4
is only -0.31, corresponding to a probability of correlation of
the order of 90 %.
In contrast, considering the (logD, [Fe/H]) plot for the
same sample of GCs, the correlation coefficient
is still -0.43, corresponding to a probability of correlation of 96 %.
The orbits only provide evidence that the more metal-rich
halo clusters ([Fe/H] > -1.4) are concentrated towards the galactic
center (Dp < 3 kpc). Therefore, these new data do not
really confirm the suggestion made by Freeman & Norris (1981).
New perigalactic distances would be helpful to give a definitive
answer to the existence of a link between the perigalactocentric
distances and the metallicities of galactic halo GCs.
6. Conclusions
|
The self-enrichment model of galactic halo GCs (see Paper I for
a detailed description) has been compared
to the observational situation and the conclusions are as follow:
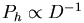 and
and
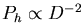 respectively.
The second solution is in better agreement with the observed
metallicity range.
Moreover, when the Murray & Lin (1992) pressure distribution is used,
the theoretical metallicity interval over the galactocentric range
1
respectively.
The second solution is in better agreement with the observed
metallicity range.
Moreover, when the Murray & Lin (1992) pressure distribution is used,
the theoretical metallicity interval over the galactocentric range
1  Dkpc
Dkpc  30 is
-2.65
30 is
-2.65  [Fe/H]
[Fe/H]  -1.15.
This result is in nice agreement with the observations
in the galactic halo GCs.
-1.15.
This result is in nice agreement with the observations
in the galactic halo GCs.
7. Figures
|
 Figure 1 |
 Figure 2 |
 Figure 3 |
 Figure 4 |
Acknowledgements
|
This research was supported by contracts Pôle d'Attraction Interuniversitaire P4/05 (SSTC, Belgium) and FRFC F6/15-OL-F63 (FNRS, Belgium).
References
|
Brown J.H., 1993, In: Smith G.H., Brodie J.P. (eds) ASP Conference
Series Volume 48, The globular clusters-galaxy connection, p. 766
Brown J.H., Burkert A., Truran J.W. 1991, ApJ 376, 115
Brown J.H., Burkert A., Truran J.W. 1995, ApJ 440, 666
Buonanno R., Corsi C.E., Fusi Pecci F., Richer H.B., Fahlman G.G.
1993, AJ 105, 184
Buonanno R., Corsi C.E., Fusi Pecci F., Richer H.B., Fahlman G.G.
1995a, AJ 109, 650
Buonanno R., Corsi C.E., Pulone L., Fusi Pecci F., Bellazini M. 1998,
A&A 333, 505
Carignan C., Beaulieu S., Freeman K. 1990, AJ 99, 178
Carney B.W., Laird J.B., Latham D.W., Aguilar L.A. 1996, AJ 112, 668
Cayrel R. 1986, A&A 168, 81
Chaboyer B., Demarque P., Sarajedini A. 1996, ApJ 459, 558
Chiba M., 2000, In: A. Weiss, T. Abel and V. Hill (eds.)
Proceedings of the 2nd ESO/MPA Conference,
The First Stars, p. 77 (Springer)
Cô:té P. 1999, AJ 118, 406
Da Costa G.S., 1993, In: Smith G.H., Brodie J.P. (eds) ASP Conference
Series Volume 48, The globular clusters-galaxy connection, p. 363
Da Costa G.S., Armandroff T.E. 1995, AJ 109, 2533
Dinescu D.I., Girard T.M., Van Altena W.F. 1999, AJ 117, 1792
Djorgovski S., Meylan G. 1994, AJ 108, 1292
Eggen O.J., Lynden-Bell D., Sandage A. 1962, ApJ 136, 748
Elson R.A.W., Fall S.M. 1988, AJ 96, 1383
Fabricant D., Lecar M., Gorenstein P. 1980, ApJ 241, 552
Fall S.M., Rees M.J. 1985, ApJ 298, 18
Ferraro I., Ferraro F.R., Fusi Pecci F., Corsi C.E., Buonanno R. 1995,
MNRAS 275, 1057
Freeman K.C., Norris J. 1981 ARA&A 19, 319
Fusi Pecci F., Bellazini M., Cacciari C., Ferraro F.R. 1995, AJ 110,
1664
Harris W.E., Pudritz R.E. 1994, ApJ 429, 177
Harris W.E. 1996, AJ, 112, 1487
Harris W.E., Bell R.A., Vandenberg D.A., Bolte M., Stetson P.B.,
Hesser J.E., van den Bergh S., Bond H.E., Fahlman G.G., Richer H.B.
1997, AJ 114, 1030
Hartwick F.D.A., 1987, In: The Galaxy; Proceedings of the NATO
Advanced Study Institute, Cambridge, England, Dordrecht,
D. Reidel Publishing Co., p. 281-290.
Ibata R.A., Wyse F.G.A., Gilmore G., Irwin M.J., Suntzeff N.B. 1997,
AJ 113, 634
Irwin M.J., Demers S., Kunkel W.E. 1995, ApJ 453, 21
Jehin E., Magain P., Neuforge C., Noels A., Parmentier G.,
A. Thoul 1999, A&A 341, 241
Johnston K. V., Majewski S. R., Siegel M. H., Reid I. N. and Kunkel W. E.
1999, AJ 118, 1719
Jurcsik J. 1998, ApJ 506, L113
King I.R. 1962, AJ 67, 471
King I.R., 1999, In: Martinez Roger C., Pérez Fournon I., Sanchez F.
(eds) Cambridge University Press, Globular Clusters, p. 1
Larson R.B., 1992, In: Tenorio-Tagle G., Prieto M., Sanchez F. (eds)
Cambridge University Press,
Star Formation in Stellar System, p. 143
Lee Y.W., 1993, In: Smith G.H., Brodie J.P. (eds) ASP Conference
Series Volume 48, The globular clusters-galaxy connection, p. 142
Lee Y.W., Demarque P., Zinn R. 1994, ApJ 423, 248
Lin D.N.C., Richer H.B. 1992, ApJ 388, L57
McLaughlin D.E., Pudritz R.E. 1996, ApJ 469, 194
Majewski S.R. 1992, ApJS 78, 87
Majewski S.R. 1994, ApJ 431, L17
Majewski S.R., 2000, In: A. Noels, P. Magain, D. Caro,
E. Jehin, G. Parmentier, A. Thoul (eds.) 35th Liège
International Astrophysics Colloquium, The galactic halo:
from globular clusters to field stars, p 619
Marquez A., Schuster W.J. 1994, A&AS 108, 341
Mateo M. 1998, ARA&A 36, 435
Meylan G., Heggie D.C. 1997, A&AR 8, 1
Meylan G., 2000, In: A. Noels, P. Magain, D. Caro,
E. Jehin, G. Parmentier, A. Thoul (eds.) 35th Liège
International Astrophysics Colloquium, The galactic halo:
from globular clusters to field stars, p 543
Meziane K., Colin J. 1996, A&A 306, 747
Mighell K.J., Rich R.M., Shara M., Fall S.M. 1996, AJ 111, 2314
Minniti D. 1995, AJ 109, 1663
Murray S.D., Lin D.N.C. 1992, ApJ 400, 265
Odenkirchen M., Brosche P., Geffert M., Tucholke H.-J. 1997
New Astronomy 2, 477
Parmentier G., Jehin E., Magain P., Neuforge C., Noels A., Thoul A.A. 1999,
A&A 352, 138
Press W.H., Teukolsky S.A., Vetterling W.T. and Flannery B.P. 1992,
Numerical Recipes (2nd ed.; Cambridge Univ. Press)
Pryor C., Meylan G. 1993, In: S.G. Djorgovski, G. Meylan (eds)
ASP Conference
Series Volume 50, Structure and Dynamics of globular clusters, p. 370
Rees M.J., Ostriker J.P. 1977, MNRAS 179, 541
Rosenberg A., Saviane I., Piotto G., Aparicio A. 1999, AJ 118, 2306
Sarajedini A., Geisler D. 1996, AJ 112, 2013
Sarajedini A. 1997, AJ 113, 682
Sarajedini A., Chaboyer B., Demarque P. 1997, PASP 109, 1321
Searle L., Zinn R. 1978, ApJ 225, 357
Stetson P.B., VandenBerg D.A., Bolte M., Hesser J.E., Smith G.H.
1989, AJ 97, 1360
Stetson P.B., VandenBergh D.A., Bolte M. 1996, PASP 108, 560
Stetson P.B., Bolte M., Harris W.E., Hesser J.E., van den Bergh S.,
VandenBergh D.A., Bell R.A., Johnson J.A., Bond H.E., Fullton L.K.,
Fahlman G.G., Richer H.B. 1999, AJ 117, 247
Sutherland R.S., Dopita M.A. 1993, ApJS 88, 253
Terndrup D.M., Popowski P., Gould A., Rich R.M., Sadler E.M.
1998 AJ 115, 1476.
Van Den Bergh S. 1995, AJ 110, 1171
White S.D.M., Kauffmann G., 1994, In: Munoz-Tunon C., Sanchez F. (eds)
Cambridge University Press,
The Formation and Evolution of Galaxies, p. 471
Zinn R. 1985, ApJ 293, 424
Zinn R., 1993, In: Smith G.H., Brodie J.P. (eds) ASP Conference
Series Volume 48, The globular clusters-galaxy connection, p. 38
Institut d'Astrophysique et de
Géophysique de l'
Université de Liège
Avenue de Cointe, 5
B-4000 Liège, BELGIQUE
Tel: +32 (0)4 252.99.80
Fax: +32 (0)4 252.74.74
Web pages:
Sandrine Sohy