Le CIEL - Bulletin de la Société Astronomique de Liège Volume 62 (Décembre 2000), p.311

Les mirages gravitationnels (III)

Jean et Anna Surdej
Adaptation: André Lausberg

Dans un premier article, publié dans Le CIEL de septembre 2000, nous avons décrit certains effets de mirages atmosphériques dus à la variation de l'indice de réfraction de l'air au voisinage du sol surchauffé. On obtenait notamment la multiplication des images d'une source distante, leur déformation et leur amplification.

La théorie de la Relativité Générale d'Einstein prévoit que les rayons lumineux sont déviés au voisinage d'une masse suffisamment compacte, comme celle du Soleil, d'une galaxie ou d'un amas de galaxies. Dès lors, une grande concentration de masse peut agir comme une sorte de lentille, appelée lentille gravitationnelle. Dans le bulletin de novembre, nous avons décrit l'histoire de cette découverte, à la fois du point de vue de la théorie et aussi des observations.

Dans ce troisième article, nous reviendrons plus en détail sur le phénomène de lentille gravitationnelle, en insistant sur les effets qu'il est possible d'observer. Ensuite, nous présenterons une expérience de lentille optique, permettant de simuler en laboratoire les phénomènes réellement observés dans l'Univers.

Il sera dès lors très intéressant de comparer une série d'images obtenues soit par simulation, soit par observation directe.

Nous terminerons par un aperçu des autres résultats pouvant être déduits de ces observations, à savoir la détermination de la constante de Hubble, ainsi que celle de la distribution des masses dans des régions traversées par les rayons lumineux émis par les quasars lointains.

Action des lentilles gravitationnelles

Dans le cas des rayons provenant d'étoiles lointaines et rasant la surface du Soleil, nous avons vu que la déviation produite était de l'ordre de deux secondes d'arc. L'angle de déviation étant directement proportionnel à la masse du « déflecteur » et inversement proportionnel à son rayon, on peut s'attendre à trouver une déviation du même ordre de grandeur dans le cas d'une galaxie comme la nôtre, dont la masse est quelques centaines de milliards de fois celle de notre Soleil, et dont le rayon de la partie centrale est également quelques centaines de milliards de fois plus grand que le rayon du Soleil. Dans le cas de déflecteurs constitués par des amas de galaxies, on atteindra des déviations de l'ordre de quelques dizaines de secondes d'arc.

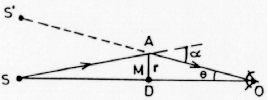
Figure 1: Dans le cas d'un alignement parfait de la source S, du déflecteur D et de l'observateur O, une masse M produit, sur un rayon passant à une distance r du centre du déflecteur, une déviation mesurée par l'angle . Si l'observateur peut voir le déflecteur, il mesure alors un écart angulaire entre d'une part ce déflecteur (et donc aussi la source réelle S) et l'image reçue de la source S'.

Comme on l'a vu dans le cas du Soleil, l'angle de déviation est donné par:

L'écart angulaire peut être calculé successivement dans les triangles ODA et OSA, en tenant compte du fait que les angles sont très petits (la tangente peut alors être égalée à l'angle exprimé en radians). On obtient:
et

Dans le cas envisagé ici, celui de l'alignement parfait des trois points S, D et O, et si les conditions sont réunies pour que le rayon représenté sur le schéma atteigne effectivement l'observateur, il en sera de même dans tous les plans contenant la droite SDO: autrement dit, l'observateur verra un anneau circulaire centré sur le déflecteur. C'est ce qu'on appelle l'« anneau d'Einstein » dont la dimension dépend de l'écart angulaire . Le carré de cet écart est obtenu à partir des trois formules précédentes:

Envisageons un cas simple, celui d'une source S située environ deux fois plus loin que le déflecteur, une situation qui a de bonnes chances d'être réalisée de temps à autres dans notre univers. Dans ce cas et la formule d'Einstein devient:

On voit donc que le carré du rayon angulaire de l'anneau d'Einstein est proportionnel à la masse du déflecteur, et inversement proportionnel à la distance entre la source et le déflecteur.

Prenons deux exemples numériques: pour une galaxie-déflecteur plus massive que la nôtre, distante de 3 milliards d'années-lumière, et dont le noyau central contient l'équivalent de mille milliards de masses solaires, avec un noyau de rayon égal à environ 15.000 années-lumière, le rayon de l'anneau d'Einstein vaut deux secondes d'arc.

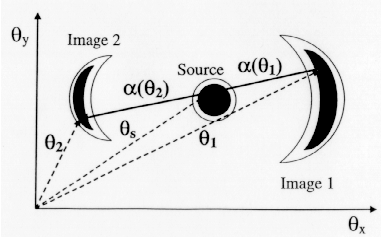
Figure 2: Les observations sont ici décrites dans un plan (, ) perpendiculaire à la ligne de visée. En l'absence de déflecteur, la source serait vue à une distance angulaire de l'origine (choisie arbitrairement), sous forme d'un double disque. Suite à la présence du déflecteur, on voit deux images 1 et 2, lesquelles ont subi des déviations correspondant à deux valeurs différentes de l'angle . La surface totale de ces deux images est supérieure à la surface du disque central.

Pour un amas de galaxies contenant cent fois plus de masse, et placé à la même distance, avec un rayon de 300.000 années-lumière, ~20 secondes d'arc. Ce sont les ordres de grandeur que nous annoncions au début de cet article.

La possibilité d'observer l'anneau d'Einstein est bien sûr extrêmement faible. Par contre, les cas d'un alignement approximatif entre la source, le déflecteur et l'observateur sont beaucoup moins rares. La figure 2 illustre cette situation, dans laquelle des fragments d'anneaux sont observés.

L'effet du déflecteur est donc à la fois de dédoubler l'image, de la déformer, et de produire deux images dont la surface totale, et donc aussi le flux observé, est supérieur à celui de l'image non déformée. Il y a donc un phénomène d'amplification que l'on peut calculer et aussi mesurer sur les clichés.

Remarquons que dans le cas de l'anneau d'Einstein, la surface totale de l'anneau est également supérieure à la surface de la source vue sans déviation; il y a donc amplification du flux observé. D'une manière générale, ce phénomène d'amplification, a priori très étonnant, s'explique par le fait que l'observateur reçoit des rayons lumineux qui normalement seraient parvenus dans d'autres régions; la lentille gravitationnelle ne fait donc que redistribuer les rayons d'une manière différente entre les différentes régions où les observateurs sont susceptibles de se trouver.

L'exemple illustré ci-dessus correspond à une des nombreuses possibilités d'images résultant de l'action des lentilles gravitationnelles. Dans une étude plus complète, sortant du cadre de cet article, il faudrait d'abord considérer un déflecteur avec une répartition de masse diffuse, au lieu d'une masse ponctuelle; dans ce cas, il serait nécessaire de remplacer dans les formules précédentes la masse totale M du déflecteur par une fonction M(r) correspondant à la masse déviant le rayon lumineux passant à la distance r du centre du déflecteur. Ensuite, il faudrait abandonner le modèle d'un déflecteur à symétrie sphérique, afin de mieux rendre compte de la forme d'une galaxie ou d'un amas de galaxies qui dévient les rayons lumineux.

Simulation des mirages gravitationnels par des lentilles optiques

Il existe une technique relativement simple, permettant de produire en laboratoire, à partir d'une source ponctuelle, une grande variété d'images multipliées, déformées et amplifiées.

Le but étant d'imiter au mieux l'action gravitationnelle qu'une masse exerce sur un rayon lumineux, on construira une lentille capable de dévier la lumière suivant la même loi, c'est-à-dire avec un angle de déviation diminuant avec la distance par rapport à l'axe optique. Il ne peut évidemment pas s'agir d'une lentille convergente ordinaire, car dans ce cas les rayons sont d'autant plus déviés qu'ils sont au départ éloignés de l'axe optique, ce qui permet d'ailleurs de focaliser ces rayons vers un seul point (Figure 3).

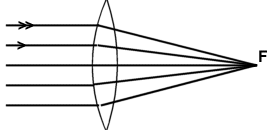
Figure 3: Dans une lentille optique convergente, les rayons arrivant sur la lentille, parallèlement à l'axe optique, sont d'autant plus déviés qu'ils sont éloignés de cet axe.

Il faut donc rechercher un système optique capable de dévier les rayons pour les rapprocher de l'axe optique, par exemple en raison inverse de leur distance à cet axe, dans le cas d'un déflecteur ponctuel, ou suivant une loi plus compliquée, si l'on veut imiter l'action des déflecteurs possédant une répartition de masse diffuse. On choisira d'abord le plus simplement des lentilles optiques à symétrie axiale, et possédant une face plane. L'autre face aura une surface calculée en fonction de la loi de déviation souhaitée.

Rappelons-nous l'histoire de l'oeuf de Colomb: pour faire tenir un oeuf immobile, avec son grand axe vertical, il suffit de casser l'oeuf (dur) sur une pointe. La première découverte d'une «lentille optique- gravitationnelle» a dû se faire lors d'une soirée bien arrosée, un des convives gardant en main le pied d'un verre brisé, et s'en servant pour regarder la flamme d'une bougie!?

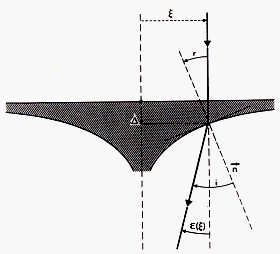
Figure 4: Déviation d'un rayon lumineux, parallèle à l'axe optique à une distance . Le rayon quitte la surface inférieure en s'écartant de la normale; la déviation =i-r dépendra de la forme de cette surface inférieure. Dans cet exemple, on peut voir que la déviation diminue quand le rayon incident s'éloigne de l'axe optique.
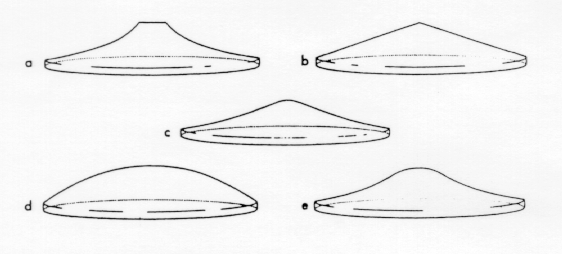
Figure 5: Exemples de lentilles optiques à symétrie axiale, permettant de simuler les déviations de rayons lumineux produites par une masse ponctuelle (a), une sphère isotherme (b), une galaxie spirale (c), un disque uniforme (d) et un disque uniforme tronqué (e)

La figure 4 nous montre cette lentille en forme de pied de verre à vin, avec un rayon venant du haut, à une distance donnée de l'axe optique. Suivant la loi de Descartes, le rayon sortant s'écarte de la normale à la surface courbe. Il suffit dès lors de calculer la forme de la surface de manière à imiter parfaitement la loi de déviation valable pour une lentille gravitationnelle.

On a ainsi établi la forme de lentilles capables d'imiter la déviation des rayons lumineux produite par divers types de déflecteurs (Figure 5). Ce genre de lentilles, faisant penser à de quelconques soucoupes volantes, ont effectivement été construites par les auteurs de cet article, et utilisées aux fins de reproduire des images de lentilles gravitationnelles.

Voici, en figure 6, le montage du banc optique comprenant, à gauche, la source de lumière, au centre la lentille optique, suivie d'un premier écran percé d'un trou d'épingle (pinhole), représentant la surface du récepteur utilisé par l'observateur. Sur l'écran de droite, on aperçoit l'image recueillie, en l'occurrence 4 images de la même source ponctuelle.**

La figure 7 permet de comparer les images obtenues d'une part à l'aide de ce dispositif de simulation, et d'autre part par l'observation des mirages gravitationnels La colonne de gauche (images a-g) montre les images observées sur le premier écran percé du trou d'épingle. Dans les deux premiers cas (a-b), la lentille optique est à symétrie axiale; dans les autres cas (c-g) elle est dissymétrique. La colonne du centre présente les images recueillies sur l'écran de droite, successivement en anneau elliptique ressemblant à un anneau d'Eintein (h), une image dédoublée et amplifiée (i), une quadruple image semblable au mirage gravitationnel connu sous le nom de «croix d'Einstein» (j), et ensuite d'autres exemples correspondant à diverses formes de mirages optiques. Dans la colonne de droite, on trouve des mirages gravitationnels de formes comparables aux mirages optiques. Les images (p, r, s, t) ont été obtenues au moyen du Télescope Spatial Hubble (HST), les autres grâce à des télescopes terrestres. L'image (s) est particulièrement intéressante car on peut y repérer le déflecteur responsable du dédoublement. Le mirage est présenté en figure 8.(* ESO et VLA/NRAO).

Ce tableau, d'un grand intérêt didactique, a été établi par Anna et Jean Surdej, avec l'aide de Sjur Refsdal. La ressemblance entre les images obtenues par simulation optique et celles réellement observées dans le ciel profond est assez extraordinaire. Bien sûr, les spécialistes ne se contentent pas d'une pareille ressemblance. Les formules mathématiques utilisées pour la confection de lentilles optiques permettent également de construire un modèle géométrique pour le déflecteur réel, constitué d'une galaxie ou d'un amas de galaxies. Parfois le déflecteur est lui-même apparent sur le cliché photographique, ce qui permet d'affiner le modèle (figure 8).

Figure 8

Ainsi, à partir d'images multiples, d'arcs ou d'anneaux, les chercheurs reconstituent les chemins suivis par les rayons lumineux émis par un quasar lointain. Plus de 50 images multiples de quasars sont aujourd'hui certifiées; on a notamment vérifié que ces images multiples proviennent bien de la même source, en comparant les différents spectres. Parfois de légères différences apparaissent, que l'on explique alors par le fait que les divers rayons ont traversé des régions différentes du déflecteur, que ce soit une galaxie ou un amas.

Une fois acquise la certitude que plusieurs images correspondent au même quasar, les chercheurs obtiennent de précieux renseignements sur la forme et la masse du déflecteur. Voici donc un outil puissant permettant de «peser» ce déflecteur, notamment quand il s'agit d'un amas de galaxies, pouvant contenir une quantité importante de « masse cachée ».

Ce domaine de recherche ouvre ainsi de nouvelles voies pour la cosmologie: outre la mise en évidence de masses cachées, on peut citer la détermination de la fameuse « constante de Hubble » H_o. Rappelons que la loi de Hubble, sous sa forme la plus simple, nous dit que la vitesse d'éloignement d'une galaxie est proportionelle à cette constante, ainsi qu'à la distance de la galaxie par rapport à nous (=H_oD). Les observateurs déterminent la vitesse grâce à la mesure précise du redshift, autrement dit le décalage spectral vers le rouge affectant les raies émises par la source qui s'éloigne. La distance D est (difficilement) estimée à partir d'indicateurs parmi lesquels on peut citer les céphéides et les supernovae.

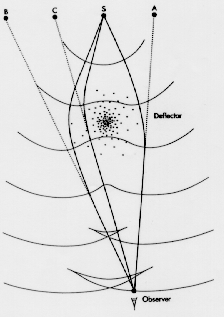
Figure 9

Il existe également des lois indiquant comment la distance varie avec la luminosité apparente d'une galaxie, ou encore son diamètre apparent. Toutes ces études aboutissent évidemment à formuler la loi de Hubble sous une forme bien plus compliquée, qui dépend du modèle d'univers considéré. De toute façon, la loi obtenue fait intervenir la constante de Hubble, dont la valeur précise est très difficile à obtenir. Rappelons que l'inverse de la valeur de H_o permet d'obtenir un ordre de grandeur pour l'âge probable de notre univers.

L'étude des mirages gravitationnels fournit un moyen tout à fait nouveau pour la détermination de H_o. La méthode est basée sur la mesure d'un décalage temporel qui parfois se manifeste entre les diverses images d'une même source. Comme le montre la figure 9, dans le cas des trois images A, B, C observées à partir d'une source S, les rayons lumineux ont parcouru des distances notablement différentes avant d'arriver à l'observateur.

De surcroît, les mêmes rayons traversent des puits de potentiel gravifiques différents lorsqu'ils passent à proximité du déflecteur, et se propagent ainsi, par rapport à l'observateur, avec des vitesses légèrement différentes, toutes d'ailleurs inférieures à 300000 km/s. C'est comme si l'environnement du déflecteur pouvait être caractérisé par un indice de réfraction variable ... et achromatique.

Si par chance la source S présente des variations temporelles de lumière, celles-ci se manifesteront à des moments différents sur les enregistrements. Or le calcul des longueurs parcourues fait intervenir immanquablement la constante de Hubble. Celle-ci, en retour, pourra être mesurée à partir des décalages temporels obtenus. Signalons qu'un décalage temporel de plus d'un an a été observé!

Comme indiqué dans le deuxième article, une première détermination a fourni la valeur H_o=63±7 km/sec/Mpc, soit une valeur inférieure à celle qui a été fréquemment citée durant les cinquante dernières années. Cette valeur relativement faible de H_o, qui semble confirmée par les études récentes de certaines supernovae, aboutit à revoir à la hausse l'âge présumé de l'Univers, avec une valeur de plus de 13 milliards d'années. Ceci n'est pas pour déplaire aux astrophysiciens, pour qui il semblait désagréable d'observer des étoiles plus vieilles que l'Univers ...

En conclusion, l'étude des mirages gravitationnels, après avoir mis quelques dizaines d'années à vaincre le scepticisme de certains, constitue aujourd'hui un domaine de recherche en pleine expansion. Il est désormais impossible de décrire l'Univers des galaxies en ignorant que de nombreuses images de sources lointaines ont subi maintes transformations avant de nous parvenir.

On ne peut refuser les mirages, sous peine de vivre dans l'illusion.