During the elaboration of his theory of General Relativity, Einstein (1915) predicted that a massive object curves the spacetime in its vicinity and that any particle, massive or not (cf. the photons), will move along the geodesics of this curved space. He showed that a light ray passing at a distance from an object characterized by an axially symmetric mass distribution M() (see Figure 1) will undergo a total deflection angle , expressed in radian by means of the relation

where G stands for the gravitational constant and c for the velocity of light. Adopting a given mass distribution (e.g. a constant mass in order to characterize a point-like object, the disk of a spiral galaxy, etc.), it is then trivial to construct an optical lens that deflects light rays accordingly, thus enabling us to study very simply in the laboratory the lensing properties of black holes, stars, quasars, galaxies, etc. as they exist in the Universe. We discuss this in greater details in the next section.

Before discussing the optical gravitational lens experiment, we wish to state that a sufficient condition for a gravitational lens to produce multiple images of a background source is simply that its surface mass density exceeds the critical density , which only depends on the relative distances , and , between the observer (O), the deflector (D) and the source (S) (cf. Equation (2.4)-(2.6)). It is also very easy to show that in the case of a perfect alignment between a source, an axially symmetric deflector and an observer, the latter will see the background source as a ring of light (the so-called Einstein ring) which angular radius is proportional to the square root of the mass of the deflector (cf. Equation (2.7)). For those students who are very curious, we propose hereafter the derivation of the quantities and (Exercise 2).

2.1 Exercise 2: Condition for multiple imaging and angular radius of the Einstein ring

 In the case of perfect alignment between a source (S), an axially symmetric deflector (D) and an observer (O) (see Fig. 1), we easily see that, with the exception of the direct ray propagating from the source to the observer, the condition for any other light ray to reach the observer is

as obtained from the direct application of the sine rule in the triangle SXO and assuming that the angles and remain very small. Of course, this will also be true if the real deflection angle since it will then be always possible to find a light ray with a greater impact parameter such that Eq. (2.2) is fulfilled. Expressing the angle between the direct ray and the incoming deflected ray as

and making use of Eqs. (2.1) and (2.2), we may thus rewrite the above condition as follows

i.e. the average surface mass density of the lens

evaluated within the impact parameter , must simply exceed the critical surface mass density , defined by

Let us note that the latter quantity is essentially determined by the distances between the source, the deflector and the observer.

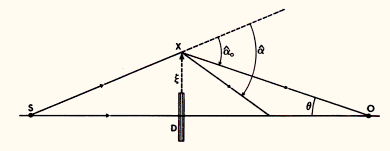
Figure 1: On the condition for an observer O to see a light ray from a distant source S, deviated by a deflector D so that more than one image can be seen. Note that O, D and S are perfectly co-aligned and that axial symmetry is assumed. No scale is respected in this diagram

Although the above reasoning essentially applies to a static Euclidian space, Refsdal (1966) has shown that it also remains valid for Friedmann, Lemaître, Robertson, Walker (FLRW) expanding universe models, provided that , and represent angular size distances. Adopting typical cosmological distances for the deflector (redshift ) and the source ( ), we find that .

Substituting M( ) and in Eq. (2.5) with a typical mass M and a radius R for the deflector, we have listed in Table 1 values for the ratio considering a star, a galaxy and a cluster of galaxies located at various distances.

 
Table 1: Ratio of the average and critical surface mass densities, angular ( ) and linear ( ) radii of the Einstein ring for different values of the mass M, distance and radius R of the deflector, assuming that (

We see that only stars and very compact, massive galaxies and galaxy clusters, for which , constitute promising `multiple imaging' deflectors.

In the case of axial symmetry, it is clear that in the presence of an efficient deflector, an observer located on the symmetry axis will actually see a ring (the so-called 'Einstein ring', cf. Fig. 10) of light from a distant source. Combining Eqs. (2.1)-(2.3), the angular radius of this ring may be conveniently expressed as

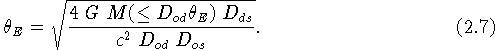
We have also listed in Table 1 typical values of for different types of deflectors located at various distances.

As we shall see in the optical gravitational lensing experiment, the value of derived above is very important because it can usually be used to estimate the angular separation between multiple lensed images in more general cases where the condition of a perfect alignment between the source, deflector and observer is not fulfilled or even for lens mass distributions which significantly depart from the axial symmetry. Knowing that angular size distances are inversely proportional to the Hubble constant , observed image separations can therefore lead to the value of , or to the value of M times the Hubble constant , if the redshifts and are known. This is the simplest and most direct astrophysical application of gravitational lensing. We see from Table 1 that for a source and a lens located at cosmological distances and ), the angle can vary from micro-arcsec (stellar deflection) to arcsec (galaxy lensing), and up to some tens of arcsec in the case of cluster lenses. Let us also finally note that the condition (2.4) for a deflector to produce multiple images of a lensed source turns out to be usually applicable, even when there is no axial symmetry.